Set
- example
- 옷장 = set
- 옷 = element
- 옷들의 일부 = subset
- 전체 옷들 = universal set
- 옷들이 몇개입니까?, 옷이 많이 있습니까? = set operations
- disjoint sets : 교집합이 공집합인 경우
- partition of $A$
- $A = \{1,2,3,4\}$, partition of $A$ : $\{ \{1,2\},\{3\},\{4\}\}$
- 겹치지 않고 합쳤을 때 전체가 되는
- cartesian product : 두 집합에서 각각 원소 하나씩을 가져와서 쌍을 만들고, 그 쌍들로 집합을 이룬 것
- $A \times B = \{(a,b) : a \in A, b \in B \}$
- power set $2^A$ : $A$가 가질 수 있는 모든 subsets들의 집합
- $A = \{1,2,3\}$
- $2^A = \{ \varnothing, \{1\}, \dots, \{1,2,3\} \}$
cardinality
: 무한끼리의 차이를 다루기 위한 개념 (countably infinite vs uncountably infinite)
- finite
- cartesian product의 cardinality : $|A| = m, |B| = n → |A \times B| = mn$
- power set의 cardinality : $|A| = n → |2^A| = 2^n$
- 두 집합에 one-to-one correspondence이 존재하면, 같은 cardinality를 가짐 (동치)
- 그래서 one-to-one correspondence이 없음을 보이면 다른 cardinality를 가진다는 것을 보일 수 있음
- contable
- countable (countably infinite) : 어떤 집합이 셀 수 있는 집합(set of natural numbers)과 one-to-one correspondence이 있으면, 그 집합을 countable이라고 함
- 정수와 분수(rational numbers)는 countable! (why? 한 개씩 순서를 매길 수 있어서)

- denumerable : countably infinite
- denumerable set들은 같은 cardinality를 가짐
- $\aleph_0$ (aleph null 이라 부름)
- 이게 뭐냐면 그냥 자연수의 개수(무한대)
- uncountable
- $\mathbb{c} = 2^{\aleph}$ (continuum 이라 부름)
- 0과 1사이에 있는 실수의 개수는 몇개인가? 무한개 → 그럼 정수의 개수와 같나? → NO
📎 Cantor's Diagonal Argument: The Cardinality of $[0, 1]$ is Uncountable
Proof Sketch (귀류법)
1. $\mathcal{C}$가 countable하다고 가정
2. Countable하다는 것은 $\mathcal{S} = \{x_1, x_2, \dots\}$라는 대응되는 sequence가 존재한다는 것을 의미 (이때 sequence들의 개수는 정수의 개수와 같은 $\aleph_0$ (countably infinite)임)
3. 0과 1 사이의 숫자는 이진법으로 표현될 수 있다.
따라서 모든 숫자를 다음과 같이 나열할 수 있다고 가정한다:
$(x_1 = 0.d_{11}d_{12}d_{13}\dots)$ $(x_2 = 0.d_{21}d_{22}d_{23}\dots)$ $(x_3 = 0.d_{31}d_{32}d_{33}\dots)$
(여기서 $d_{ij} \in \{0, 1\}$)
4. 새로운 숫자 $x_{\text{new}}$를 다음과 같이 정의합니다: $(x_{\text{new}} = 0.\overline{d}_1\overline{d}_2\overline{d}_3\dots)$
여기서 $\overline{d}_i = 1 - d_{ii}$
즉, $x_{\text{new}}$는 대각선 요소 $d_{ii}$를 뒤집어 생성된 숫자
5. $x_{\text{new}}$는 $\mathcal{S}$에 포함되지 않는다:
$x_{\text{new}}$는 $\mathcal{S}$의 어떤 숫자와도 일치하지 않기 때문이다.
이는 우리가 countable하다고 가정한 것과 모순임
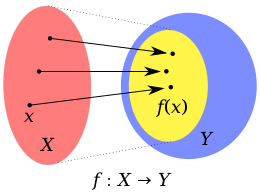
function or mapping $f: U → V$
- $U$ : domain (정의역)
- $V$ : codomain (함수값으로 나올 수 있는 값의 집합, 공역)
- $f(A)$ : image ($A$라는 입력으로 나오는 값, codomain의 subset, 치역)
- $f(A) = \{ f(x) \in V : x \in A \}, A \subseteq U$
- $f(U)$ : range (domain $U$의 전체 set에 대해 나오는 codomain $V$의 공간)
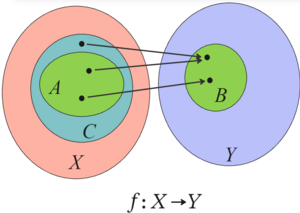
- $f^{-1}(B)$ : inverse image or preimage
- $f^{-1}(B) = \{ x \in U : f(x) \in B \}, B \subseteq V$
- 강아지/고양이 사진에서 라벨을 찾는 문제와 동일
- one-to-one or injective
- $f(a) = f(b) ⇒ a=b$
- onto or surjective
- $f(U) = V$
- codomain을 다 커버하는 경우
- invertible
- one-to-one and onto
728x90
'AI > bayesian optimization' 카테고리의 다른 글
| 인공지능 및 기계학습 심화 | [2-20] Acquisition Function 2 (0) | 2024.11.18 |
|---|---|
| 인공지능 및 기계학습 심화 | [2-19] Acquisition Function 1 (0) | 2024.11.18 |
| Posterior Predictive Distribution (0) | 2024.11.17 |
| MAP (1) | 2024.11.14 |
| MLE (0) | 2024.11.14 |




댓글