Roman Garnett | 5.2 sequential decisions with a fixed budget

detour : posterior predictive distribution

$$ p(y{\prime} | x, \mathcal{D}) = \int p(y{\prime} | x, \phi) p(\phi | x, \mathcal{D}) \, d\phi $$

 

이 식은 $ y' $에 대한 posterior predictive distribution이다.

모든 가능한 파라미터 $\phi$값을 그들의 개연성(plausibility)에 따라 가중치로 적분함으로써 posterior predictive distribution은 자연스럽게 미지의 objective function 값에 대한 uncertainty를 반영한다.

>> 이게 무슨 말?

 

 

 

 

 

 

 

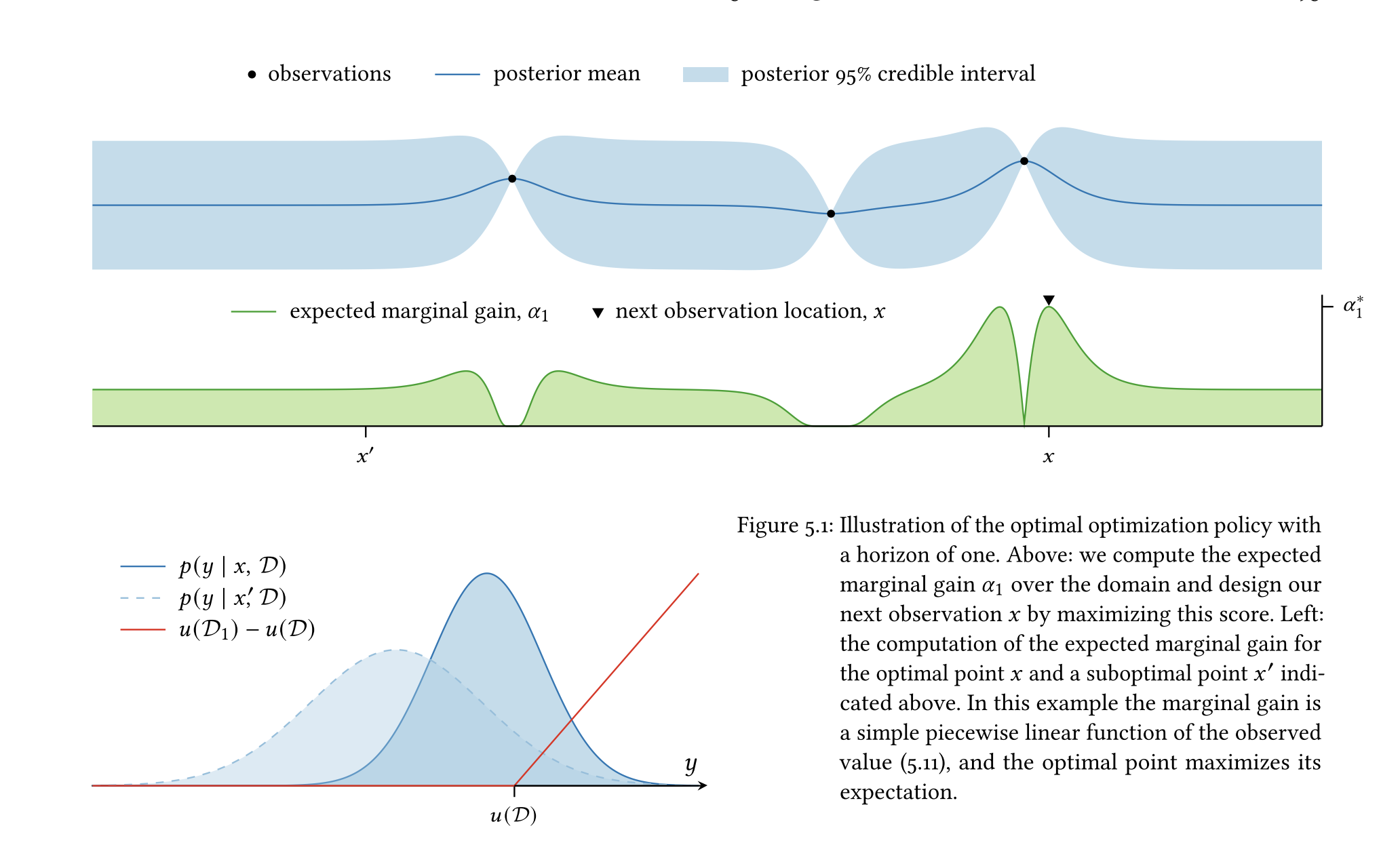
추가예정

@book{garnett2023bayesian,
  title={Bayesian optimization},
  author={Garnett, Roman},
  year={2023},
  publisher={Cambridge University Press}
}