
Bayesian에 대해 드디어 제대로 공부를 해보려고 한다..
공부를 하기에 앞서 교재는 Bayesian Optimization Theory and Practice Using Python 로 정했다.
1. BO (Bayesian Optimization)
Beyesian Optimization은 말 그대로 Bayesian approach로 optimization problem을 푸는 것이다.
그럼 Optimization의 목적이 무엇이냐 물으면 search domain안에서 optimal objective value를 찾는 것을 목표로 한다.
search process는 specific initial location으로 시작하고 particular policy에 따라서 다음 sampling할 location을 반복적으로 찾고, 새로운 observation을 수집하고, 안내하는 policy를 갱신한다.
여기서 sampling이란, 탐색하고자 하는 함수 $f(x)$의 특정 위치 $x$에서 함수를 '평가'하는 과정을 의미한다. 이는 매우 중요한 과정으로, 샘플링을 통해 새로운 데이터 포인트를 얻고, 이 데이터를 바탕으로 함수의 형태와 optimum을 추정하게 된다.

그림 1-1에 나타난 것과 같이, 전체 최적화 과정은 policy와 environment 간의 반복적인 상호작용으로 구성된다.
여기서 policy는 새로운 input에 대한 observation을 받아들여 원칙에 따라 다음 샘플링 위치를 출력하는 mapping function임. 이것은 끊임없이 학습되고 개선된다. 좋은 policy는 global opimum으로의 탐색을 더 효율적이고 효과적으로 안내하기 때문에 중요하다.
반면, environment은 policy에 의해 특정 경계 내에서 학습될 미지의 objective function을 포함한다. policy에 의해 요청한대로 함수 값을 조사할 때, 종종 노이즈로 인해 실제 관찰 값이 오염되어 학습을 어렵게 될 때가 있다.
따라서, 베이지안 최적화는 노이즈로 오염된 알려지지 않은 환경에서 가능한 한 빨리 global optimum에 효율적으로 도달할 수 있도록 정책을 학습하고자 한다.
2. Objective Function
베이지안 최적화에서 objective function은 다음과 같은 특성을 가지고 있다.
1. black box function
목표함수의 명시적 표현 (explicit expression)을 알 수 없기 때문에 함수가 어떻게 생겼는지 모른다.
함수의 내부 구조나 수학적 식은 알 수 없지만, 특정 위치에서 함수 값을 sampling하여 평가할 순 있다.
2. noise
종종 노이즈로 인해 해당 위치의 실제 값이 정확하지 않을 수도 있다. 따라서 목표 함수의 실제 값을 간접적으로 평가하게 되며, 환경으로부터의 실제 관찰 값에 내재된 이런 노이즈를 고려해야 한다.
>> 그래서 함수 평가시 노이즈를 포함시켜서, 관찰된 값의 '불확실성'을 모델링해야 한다. 여기서 Gaussian Process를 사용하여 불확실성을 정량화한다.
3. functional evaluation is costly
함수 평가는 비용이 많이 들기에 모든 위치를 조사하는 것은 불가능.
따라서 기존의 관찰 값을 최대한 활용하고 다음 샘플링 결정을 체계적으로 내리고, 제한된 자원을 유망한 위치에 잘 투자해야 한다. (the limited resource is well spent on promising locations)
>> 이를 위해, exploration(탐색)과 exploitation(활용) 사이의 균형을 맞추는 것이 중요하다.
4. gradient X
gradient를 사용할 수 없어, Gradient Descent와 같은 최적화 방법은 쓰지 못하고, 대신 샘플링을 통해 탐색해야 한다.
>> 그래서 기존의 관찰 데이터를 사용하여 목표 함수의 형태를 '추정'하고, 이 추정을 기반으로 새로운 샘플링 위치를 선택한다.
3. Observation Model
관찰 모델(Observation Model)은 true objective function과 actual observation과 noise 간의 관계를 형식화하는 방법이다.
- true objective function : $f(x)$ >> 궁극적으로 알고자 하는 함수
- actual observation : $y$ >> 특정 위치 $x$에서 목표함수 $f(x)$를 평가하면, 실제 관찰 값 $y$를 얻는다.
- noise : $\epsilon$ >> 일반적으로 가우시안 분포를 따른다고 가정한다.
수식으로 표현하면 다음과 같다.
$$y=f(x) + \epsilon$$
$$ \epsilon \sim N(0,\sigma^2)$$
위치 $x$와 목표 함수 값 $f$에 기반하여 관찰 값 $y$의 확률 분포는 $p(y|x,f)$로 나타내고, 이는 정책이 환경에서 관찰 값을 어떻게 보는지를 지배(govern)하는 확률 모델이다.
가우시안 관찰 모델
주어진 위치 $x$에서 실제 관찰 값 $y$는 목표 함수 값을 $f$를 평균으로 하고, 분산 $\sigma^2$를 갖는 가우시안 분포를 따른다.
$$ p(y|x,f) \sim N(y;f,\sigma^2)$$
4. Bayesian Statistics
4-1. Bayesian Inference
베이지안 추론은 베이즈룰을 이용해 세가지 구성요소 prior $p(\theta)$, likelihood $p(data|\theta)$, posterior $p(\theta|data)$ 간의 상호작용을 논리적으로 해석하는 방법이다.
$$
p(\theta \mid \text{data}) = \frac{p(\text{data} \mid \theta) \cdot p(\theta)}{p(\text{data})}
$$
사전 분포 prior과 새로운 데이터를 결합하여 파라미터를 업데이트 하여 사후분포 posterior을 형성하는 통계 방법이다.
4-2. Frequentist vs. Bayesian Approach
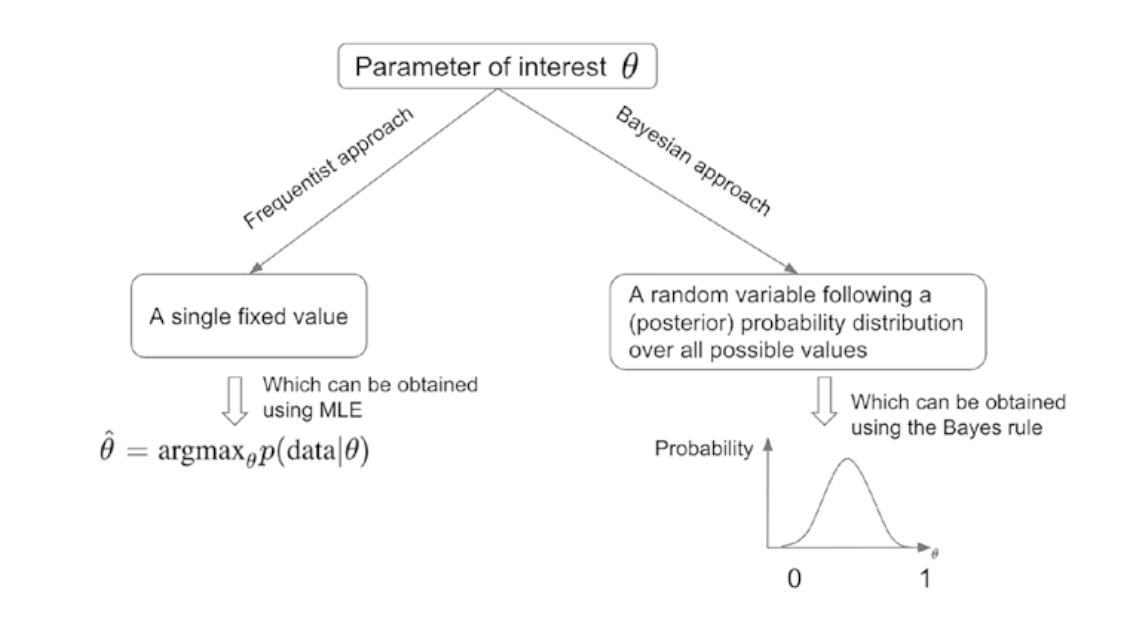
- Frequentist Approach : $\theta$를 고정된 값으로 간주. 이 고정된 값을 추정하기 위해 데이터를 사용한다. 이 접근법의 목표는 주어진 데이터를 가장 잘 설명하는 최적의 파라미터의 값을 찾는 것. 이를 위해 MLE를 사용한다. MLE는 다음과 같이 정의된다.
$$\hat{\theta} = \arg\max_\theta p(data|\theta)$$
>> 예시 : 시험 점수 데이터를 기반으로 학생들의 평균 점수를 추정할 때
- Bayesian Approach : 파라미터 $\theta$는 확률 변수로 간주, 이 값은 다양한 값을 가질 수 있고 각 값에 확률이 부여된다.
>> 시험 점수 데이터를 기반으로 학생들의 평균 점수에 대해 추론할 때, 베이지안 접근법을 사용하면 평균 점수의 분포를 알 수 있다.
4-3. Joint, Conditional, and Marginal Probabilities
간단하게 수식만 보고 가자
1. Joint Probability Distribution
두개의 random variable $x$와 $y$가 동시에 발생할 확률
$$
p(x, y) = p(x \mid y)p(y) = p(y \mid x)p(x)
$$
2. Conditional Probability Distribution
$y$가 특정 값 $Y$일 때, $x$의 확률 분포를 나타냄
$$
p(x \mid y = Y)
$$
3. Marginal Probability Distribution
이 확률 분포는 $y$를 고려하지 않고 $x$만을 고려한 확률분포이다. 베이즈룰에 의해 성립한다.
$$
p(x) = \int p(x, y) dy = \int p(x \mid y)p(y) dy
$$
'AI > bayesian optimization' 카테고리의 다른 글
| Knowledge Gradient (KG)에 대해서 (0) | 2024.09.18 |
|---|---|
| 최적화 스터디 | 1단원 bayesian optimization workflow 복습 (0) | 2024.09.18 |
| 최적화 스터디 | 9주차 : Knowledge Gradient (0) | 2024.08.20 |
| Bayesian Optimization 내맘대로 정리 (0) | 2024.05.15 |
| Gaussian Process 내맘대로 정리 (0) | 2024.05.14 |




댓글