6.1 Introducing Knowledge Gradient
Knowledge Gradient
- nonmyopic : 미래의 정보를 고려하여 현재의 최적화 결정을 내리는 접근 방식 ↔ myopic : 현재 상태에서만 최적화를 수행
- KG는 expected utility의 marginal improvement에 미치는 영향을 고려함
- marginal improvement(맨날 까먹음) : 새로운 데이터를 추가로 수집함으로써 expected utility가 얼마나 증가할 수 있는지!
- GP의 surrogate model의 posterior mean을 기반으로 한 risk-neutral perspective에서 작동
- (review) GP : 미지의 objective function의 uncertainty를 모델링함, 주어진 데이터 포인트에 대해 함수 값이 어떻게 분포할지를 추정하고 새로운 데이터 포인트에서의 함수 값 예측함 → 그게 posterior mean
- risk-neutral : 불확실성을 고려하지 않고 posterior mean만 고려해서 의사결정을 함. 분산(불확실성)을 고려하기 보단, 예상되는 평균에만 집중
utility
$$ u(\mathcal{D}n) =\mu^*{\mathcal{D}n}= \max{x \in X} \mu(x; \mathcal{D}_n) $$
(maximum 값엔 *을 붙임)
- 현재까지 수집된 데이터셋 $\mathcal{D}n$의 utility는 predictive mean function(posterior mean)인 $\mu{\mathcal{D}_n}= \mu(x;\mathcal{D}n)=\mathbb{E}(y|x, \mathcal{D}n)$ 의 maximum $\mu^*{\mathcal{D}{n}}$으로 정의함
- 위치에 관계없이 predictive mean의 최대값이 증가하면 utility도 증가함
- EI의 utility와 다른 점?
- EI : 현재 관측된 데이터셋들 중 최댓값을 utility로 정의 (noiseless)
- KG : predictive mean(posterior mean)의 최댓값을 utility로 정의
- predictive mean function의 역할?
- 우리가 알고자 하는 objective function $f(x)$에 대한 추정치(estimate)를 제공
- 즉, $\mu(x; \mathcal{D}_n)$은 $f(x)$에 대한 best average-case estimate로 해석됨
obtain an additional observation
$$ \mathcal{D}{n+1} = \mathcal{D}n \cup \{(x{n+1}, y{n+1})\} $$
- 새로운 위치 $x_{n+1}$에서 추가 관측 $y_{n+1}$을 얻었을 때, 업데이트된 데이터셋 $\mathcal{D}_{n+1}$의 utility를 알고 싶다.
- 업데이트된 데이터셋의 utility는 새로운 predictive mean의 최댓값으로 평가됨
$$ u(\mathcal{D}{n+1}) =\mu^*{\mathcal{D}{n+1}}=\max{x \in \mathcal{X}} \mu(x; \mathcal{D}_{n+1})
$$
- 새로 추가된 데이터에 기반된 improvement는 다음과 같다
$$ \mu_{\mathcal{D}{n+1}}^* - \mu{\mathcal{D}_n}^* $$
KG function
- KG는 utility의 expected marginal increase를 측정
- 이는 주어진 위치에서 관측된 새로운 값이 utility에 미치는 평균적인 영향을 나타냄
- 함수 식은 다음과 같이 정의됨
$$ \begin{align} \alpha_{KG}(\mathbf{x}; \mathcal{D}n) &= \mathbb{E}{p(y|\mathbf{x}; \mathcal{D}n)} \left[ \mu{D_{n+1}}^* - \mu_{D_n}^* \right] \tag{1} \\ &= \mathbb{E}{p(y|\mathbf{x}; \mathcal{D}n)} \left[ \mu{D{n+1}}^* \right] - \mu_{D_n}^* \tag{2} \\ &= \int \left[ \max_{\mathbf{x}' \in \mathcal{X}} \mu_{D_{n+1}}(\mathbf{x}') \right] p(y|\mathbf{x}; \mathcal{D}n) \, dy - \max{\mathbf{x}' \in \mathcal{X}} \mu_{D_n}(\mathbf{x}') \tag{3} \end{align}$$
- 수식 설명$\mu_{D_{n+1}}^* - \mu_{D_n}^*$ : 추가된 데이터에서 $\mathcal{D}_{n+1}$의 predictive mean function의 최댓값에서 현재 데이터셋 $\mathcal{D}_n$의 predictive mean을 뺀 값으로 utility의 increase(improvement?)을 뜻함(2) : $\mu_{D_{n}}^*$ 을 expectation에서 꺼냄
- (3) : expectation을 적분식으로 바꾸면 저렇게 표현 가능, $\mathbf{x}'$은 최적의 위치를 뜻함
- → 새로운 데이터를 추가한 후의 utility 증가량
- (1) : $\mathbb{E}{p(y|\mathbf{x}; \mathcal{D}n)}$ : 주어진 $x$에서의 관측한 $y{n+1}$에 대한 expectation → $y{n+1}$의 uncertainty를 반영함
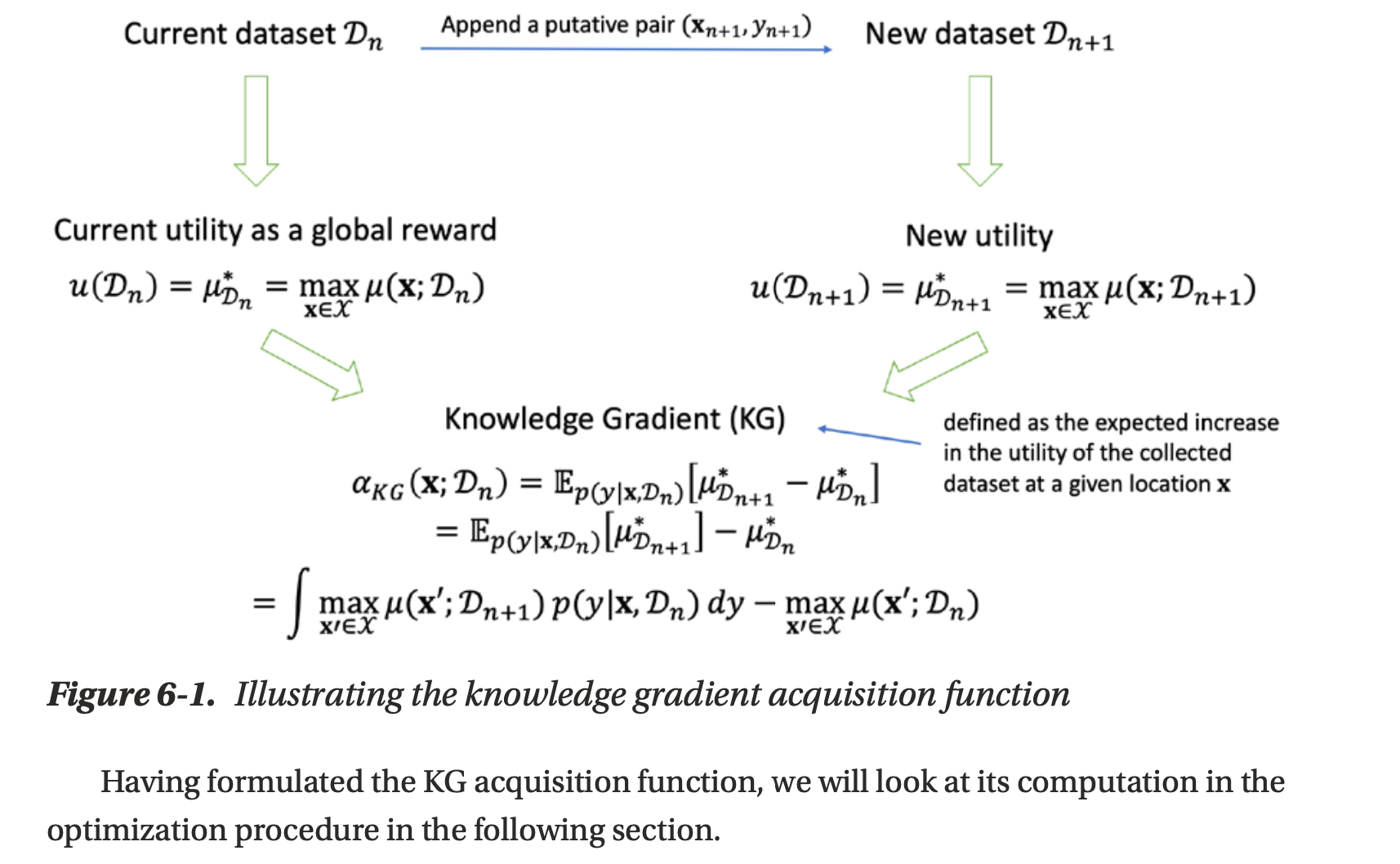
- global reward ? a mount of knowledge(지식의 양)를 전체 데이터셋 $\mathcal{D}$ 에 대한 global reward(maximum posterior mean)으로 봄
6.1.1 Monte Carlo Estimation
KG 함수는 expectation 계산이 analytic하지 않아 어려움 → 그래서 Monte Carlo Estimation을 써서 특정 위치에서 KG값을 approximation할거다
여기서는 GP모델로부터 random하게 생성된 $M$개의 샘플을 사용하여 특정 위치 $x$에서의 KG를 계산
$$
\begin{align}
\hat{\alpha}{KG}(\mathbf{x}; \mathcal{D}_n)
&= \frac{1}{M} \sum{i=1}^{M} \left( u(\mathcal{D}{n+1})^{(i)} - u(\mathcal{D}_n) \right) \
&= \frac{1}{M} \sum{i=1}^{M} \left( \mu_{D_{n+1}}^{(i)} - \mu_{D_n}^{(i)} \right)
\end{align}
$$
(\hat이 달린 이유 : 근사값이라서)
- i번째 가상 샘플 $y^{(i)}$는 현재 GP의 posterior 에 기반하여 생성됨
- → $y^{(i)} \sim p(y|x,\mathcal{D}_n)$
- $\mathcal{D}_{n+1}^{(i)} = \mathcal{D}_n \cup \{ (\mathbf{x}, y^{(i)}) \}$ : 새로운 샘플 $y^{(i)}$를 추가한 후의 데이터셋
- $u(\mathcal{D}_{n+1})^{(i)}$ : $i$번째 샘플에 대해 새로운 데이터셋의 utility
- $u(\mathcal{D}_{n})$ : 기존 데이터셋의 utility
- $\mu_{D_{n+1}}^{(i)} - \mu_{D_n}^$ : 새롭게 관측된 데이터를 포함한 후 최적의 위치에서의 기댓값 - 현재까지의 최적의 위치에서의 기댓값
- 결국 utility의 increase
- 결국 다 더한 다음 $M$으로 나눠서 평균을 구함

샘플 수 M이 증가함에 따라 근사치 $\hat{\alpha}$ 는 실제 KG $\alpha$에 더 근접하게 되고 M이 무한대로 가면 이 근사는 unbiased estimate가 된다.
KG함수를 계산할 때, predictivve mean function의 최댓값을 찾는 과정에서 L-BFGS-B와 같은 nonlinear optimization method를 쓸 수 있다. SciPy의 minimize() 함수를 이용한다. 그럼 posterior mean curve에서 global maximum을 찾는 데 유용함

각 iteration에서, 해당 위치 x에서의 posterior mean $\mu_{\mathcal{D}}(x)$과 variance $\sigma^2_{\mathcal{D}_n}(x)$을 사용하여 정규 분포를 따르는 random variable $y^{(i)}$의 실현값(realization)을 시뮬레이션해서 구함
이를 위해 standard normal distribution $\mathcal{N}(0,1)$을 따르는 random variable $z^{(i)}$를 생성
그 다음, scale-shift transformation을 적용하여 $y^{(i)}$ 값을 구한다.
$$ y^{(i)} = \mu_{\mathcal{D}n}(\mathbf{x}) + \sigma{\mathcal{D}_n}(\mathbf{x}) \cdot z^{(i)} $$
inner optimization : 추가된 데이터셋과 기존 데이터셋 사이에서의 maximum predictive mean의 차이를 평균내서 계산, maximum posterior mean 을 찾는 과정도 포함됨
outer optimization : 전체 영역에서 KG 값의 최대값을 찾는 것이 목표
'AI > bayesian optimization' 카테고리의 다른 글
| Knowledge Gradient (KG)에 대해서 (0) | 2024.09.18 |
|---|---|
| 최적화 스터디 | 1단원 bayesian optimization workflow 복습 (0) | 2024.09.18 |
| 최적화 스터디 | 1주차 : Bayesian Optimization Overview [1] (0) | 2024.06.06 |
| Bayesian Optimization 내맘대로 정리 (0) | 2024.05.15 |
| Gaussian Process 내맘대로 정리 (0) | 2024.05.14 |




댓글