이 단원에서는 순차적 의사 결정 (sequential decision-making)을 통한 최적화를 구체적으로 다룬다.
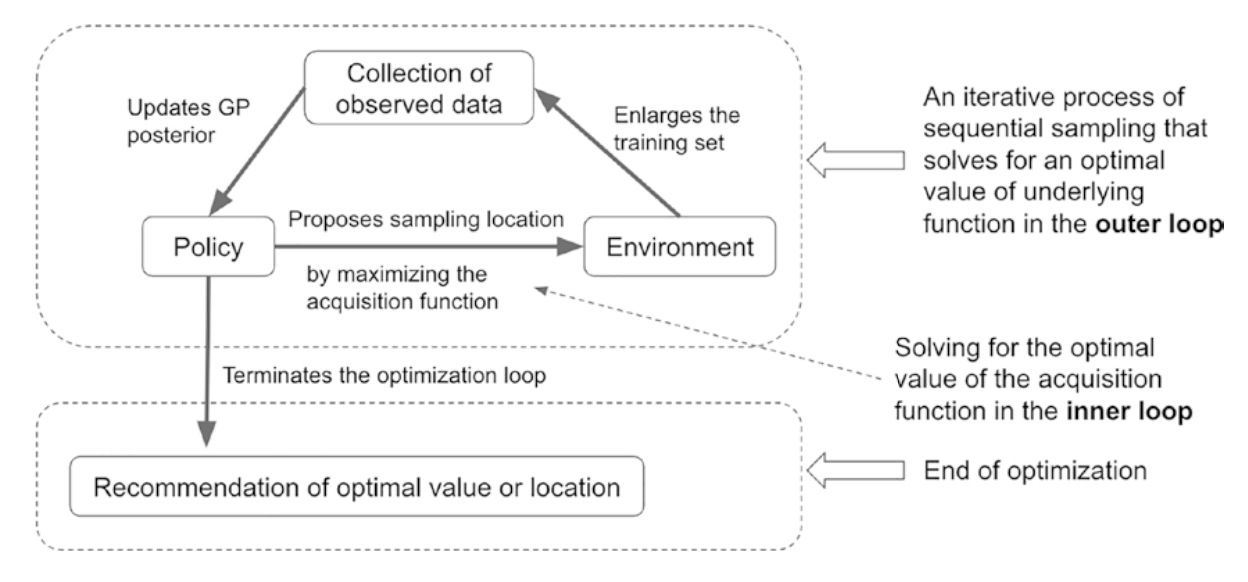
우선, 이 figure을 보자. outer loop와 inner loop가 존재한다.
1. outer loop 외부 루프에서 하는 일은?
- acquisition function을 maximize한 걸 토대로 다음 샘플링 위치를 제안함
- acquisition function이 개선(improvement)될 가능성이 있어 추가 샘플링이 필요하다고 판단되면, inner loop에 진입
- 여기서 할당된 자원(budget)이 모두 소진되면, 종료 규칙(stopping rule)에 의해 종료됨
2. inner loop 내부 루프에서 하는 일은?
- acquisition function을 maximize하는 위치를 탐색 -> 그 위치에서의 데이터를 수집함으로써 최적화 성능을 개선시킨다.
- 새로운 얻은 데이터를 바탕으로 GP의 posterior을 업데이트 -> uncertainty 정보를 반영하여 다음 샘플링에서 더 나은 결정을 할 수 있도록 policy를 개선시킨다.
Seeking the optimal policy
BO의 궁극적인 목표는 uncertainty하에서도 sequential decision-making을 잘 하는 optimal한 policy를 찾아나가는 것
acquisition function을 통해 새로운 샘플링 위치를 선택하는 방법은 다음과 같다.
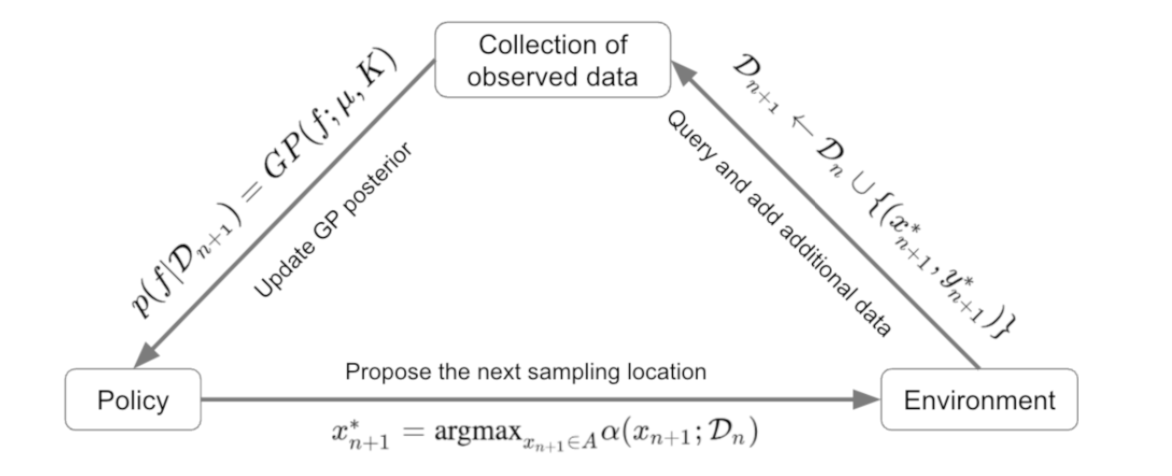
1. 다음 샘플링 위치 $x_{n+1}$은 다음과 같이 acquisition function $\alpha$를 최대화하는 위치로 정의된다:
$$ x_{n+1}^* = \underset{x_{n+1} \in A}{\arg \max} \alpha (x_{n+1}; \mathcal{D}_n) $$
2. 새로 관측한 데이터를 포함시켜 데이터셋을 업데이트한다:
$$ \mathcal{D}_{n+1} = \mathcal{D}_n \cup \left\{ \left(x_{n+1}^*, y_{n+1}^* \right) \right\} $$
3. 업데이트된 데이터를 바탕으로 GP의 posterior distribution은 다음과 같이 업데이트된다.
$$ p(f | \mathcal{D}_{n+1}) = GP(f; \mu_{n+1}, \kappa_{n+1}) $$
Utility-driven Optimization
BO의 궁극적인 목표는 global optimum에 도달할 수 있는 **가치있는** observation들을 모으는 것이다.
여기서 **가치**는 utility로 quantification된다.
즉, utility가 높은 값을 가지면 global maximum에 도달할 가능성이 있는 녀석이다.
$t=n$까지 데이터셋을 관찷했을 때, utility의 maximum값을 global maximum에 도달할 수 있는 값으로 본다:
$$ u(\mathcal{D}) = \max{y_{1:n}=y_n^*} $$
(노이즈가 없는 경우)
위의 값은 미래의 candidate observation들과 비교할 때 쓰이며, incumbent라고도 불린다.
candidate location $x_{n+1}$에서 utility를 계산하는 방법을 알아보자.
$x_{n+1}$에서 아직 관측되지 않은 값 $y_{n+1}$을 가정한 후, 해당 지점에서의 utility를 평가한다.
이때 objective function이 randomness를 가지고 있기 때문에, $y_{n+1}$는 GP모델의 posterior distribution을 따를 것이다.
따라서 $y_{n+1}$이 random variable이므로 utility의 expectation을 계산해야 한다.
익 값은 후보 지점 $x_{n+1}$와 현재까지 관측한 데이터 $\mathcal{D}_n$을 바탕으로 posterior predictive distribution을 사용하여 expected utility 값을 구한다.
아직 관찰되지 않은 데이터 $(x_{n+1},y_{n+1})$을 추가적으로 가지고 있다고 가정하면, 수식으로는 다음과 같이 나타난다:
$$ \mathbb{E}_{y_{n+1}} \left[ u(x_{n+1}, y_{n+1}, \mathcal{D}_n) | x_{n+1}, \mathcal{D}_n \right] $$
이를 계산하면 다음과 같다:
$$ \mathbb{E}_{y_{n+1}} \left[ u(x_{n+1}, y_{n+1}, \mathcal{D}_n) | x_{n+1}, \mathcal{D}_n \right] = \int u(x_{n+1}, y_{n+1}, \mathcal{D}_n) p(y_{n+1} | x_{n+1}, \mathcal{D}_n) \, dy_{n+1} $$
이렇게 expected utility를 구하게 되면 그 중에서 가장 크게 나타나는 지점 $x_{n+1}^*$ 을 다음 샘플링할 지점으로 선택한다. $x^*_{n+1}$는 다음과 같다:
$$ x_{n+1}^* = \underset{x_{n+1} \in A}{\arg\max} \, \mathbb{E}_{y_{n+1}} \left[ u(x_{n+1}, y_{n+1}, \mathcal{D}_n) | x_{n+1}, \mathcal{D}_n \right] $$
결국 expected utility를 최대화하는 optimal한 지점을 아는 것이 목표다. 그러기 위해선 적절한 utility function을 알 필요가 있다.
우리는 한 단계를 내다보고 예측하는 것(one-step lookahead)을 최적화하려고 하므로, utility의 expected marginal gain을 최대화하는 방식으로 수식이 만들어진다.
이 expected marginal gain이 acquisition function으로 작용하여 탐색을 안내하게 된다.
수식은 다음과 같다:
$$ \alpha_1(x_{n+1}; \mathcal{D}n) = \mathbb{E}{y_{n+1}} \left[ u(x_{n+1}, y_{n+1}, \mathcal{D}n) | x_{n+1}, \mathcal{D}_n \right] - u(\mathcal{D}_n) $$
$$ x_{n+1}^* = \underset{x_{n+1} \in A}{\arg\max} \, \mathbb{E}_{y_{n+1}} \left[ u(x_{n+1}, y_{n+1}, \mathcal{D}_n) | x_{n+1}, \mathcal{D}_n \right] $$
결국 expected utility를 최대화하는 optimal한 지점을 아는 것이 목표다. 그러기 위해선 적절한 utility function을 알 필요가 있다.
우리는 한 단계를 내다보고 예측하는 것(one-step lookahead)을 최적화하려고 하므로, utility의 expected marginal gain을 최대화하는 방식으로 수식이 만들어진다.
이 expected marginal gain이 acquisition function으로 작용하여 탐색을 안내하게 된다.
수식은 다음과 같다:
$$ \alpha_1(x_{n+1}; \mathcal{D}n) = \mathbb{E}_{y_{n+1}} \left[ u(x_{n+1}, y_{n+1}, \mathcal{D}n) | x_{n+1}, \mathcal{D}_n \right] - u(\mathcal{D}_n) $$
$$ x_{n+1}^* = \underset{x_{n+1} \in A}{\arg\max} \, \mathbb{E}_{y_{n+1}} \left[ u(x_{n+1}, y_{n+1}, \mathcal{D}_n) | x_{n+1}, \mathcal{D}_n \right] $$
결국 expected utility를 최대화하는 optimal한 지점을 아는 것이 목표다. 그러기 위해선 적절한 utility function을 알 필요가 있다.
우리는 한 단계를 내다보고 예측하는 것(one-step lookahead)을 최적화하려고 하므로, utility의 expected marginal gain을 최대화하는 방식으로 수식이 만들어진다.
이 expected marginal gain이 acquisition function으로 작용하여 탐색을 안내하게 된다.
수식은 다음과 같다:
$$ \alpha_1(x_{n+1}; \mathcal{D}n) = \mathbb{E}{y_{n+1}} \left[ u(x_{n+1}, y_{n+1}, \mathcal{D}n) | x_{n+1}, \mathcal{D}_n \right] - u(\mathcal{D}_n)\ $$
@book{liu2023bayesian,
title={Bayesian Optimization: Theory and Practice Using Python},
author={Liu, Peng},
publisher={Springer}
}
'AI > bayesian optimization' 카테고리의 다른 글
| 저널클럽 BO | Bellman’s Principle of Optimality (0) | 2024.10.21 |
|---|---|
| 저널클럽 BO | One-step Lookahead Policy, Multi-step Lookahead Policy (0) | 2024.10.21 |
| Knowledge Gradient (KG)에 대해서 (0) | 2024.09.18 |
| 최적화 스터디 | 1단원 bayesian optimization workflow 복습 (0) | 2024.09.18 |
| 최적화 스터디 | 9주차 : Knowledge Gradient (0) | 2024.08.20 |



댓글